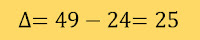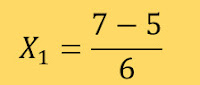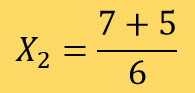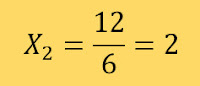Nesse grupo de exercícios vamos resolver as questões sobre coeficientes das equações do 2º grau.
01. Na a equação do 2º grau 3x² – 2x + 1 = 0, determine a soma de seus coeficientes.
A) 0
B) 1
C) 2
D) 3
E) 4
02. Determine a soma dos quadrados dos coeficientes da equação -x² – 3 = 0.
A) 4
B) 8
C) 9
D) 10
E) 16
03. Calcule o valor da expressão – 4ac sabendo que a e c são coeficientes da equação 5x² – 4x – 3 = 0.
A) 48
B) 60
C) 80
D) 100
E) 240
04. Sabendo que a, b e c são os coeficientes da equação x² – x – 1 = 0, determine o valor da expressão b² - 4ac
A) 1
B) 2
C) 3
D) 4
E) 5
05. Sendo a e b coeficientes da equação 4x² + 9 = 12x, calcule o valor da expressão – b/a.
A) 3
B) – 9/4
C) 9/4
D) – 4/3
E) 4/3
06. O IFCe em 2003-1, na época CEFET-Ce, propôs a seguinte questão em seu processo seletivo: "O produto de um número inteiro positivo pela sua quarta parte é igual a 100. Calcule esse número." Ao expressar este problema em linguagem matemática nos deparamos nos deparamos com uma equação do 2º grau da qual, depois de devidamente padronizada, podemos garantir sobre seus coeficientes:
A) a = 0
B) b = 0
C) c = 0
D) a = c = 0
E) b = c = 0
07. p(x) = x² – 50x + A = 0 , onde A ∈ ℜ. Para que o polinômio P(x) torne-se um trinômio quadrado perfeito, o valor de A é:
A) 25
B) 125
C) 225
D) 625
E) 1025
08. A soma dos coeficiente da equação (x - 4)² = 5 após a sua padronizaçao é:
A) 1
B) 2
C) 3
D) 4
E) 5
GABARITO
01. C
02. E
03. B
04. E
05. A
06. B
07. A
08. D
quinta-feira, 31 de dezembro de 2009
quarta-feira, 30 de dezembro de 2009
EQUAÇÕES DO 2º GRAU - AULA 03
1. RESOLUÇÃO DAS EQUAÇÕES COMPLETAS
Para determinar o conjunto-verdade de uma equação do 2º grau recomenda-se transformá-la noutra equivalente de modo a fique positivo e na busca da adequação à fórmula reduzida ao padrão, ou seja, enfatizando que uma equação do segundo grau deve ser escrita como:
ax2 + bx + c = 0
e usa-se então a conhecida fórmula de Bhaskara conforme a figura que segue:
O binômio b2 - 4ac chama-se discriminante e representa-se pela letra grega Δ (lê-se delta). Assim temos:
Δ = b2 - 4ac
A nossa fórmula ficará então:
Este Δ(o discriminante) pode ser positivo, negativo ou nulo. Vejamos como exemplo a equação
(x - 2)2 - 1 = 0
Como se percebe, esta equação não está no formato padronizado sen, portanto, necesário a sua devida organização e, para tanto vamos começar efetuando o quadrado da diferença indicada.
x2 - 2.x.2 + 22 - 1 = 0
x2 - 4x + 4 - 1 = 0
x2 - 4x + 3 = 0
Agora sim, a equção que temos está padronizada e pronta para identificarmos os seus coeficientees que são: a = 1, b = - 4 e c = 3
Podemos, então,substituir os valores do coeficientes na fórmula do cálculo do Δ
Lembrando que : Δ = b2 - 4ac
Δ = (-4)2 - 4.1.3
Δ = 16 - 12
Δ = 4
e, como vemos Δ > 0
Estamos prontos para substituir na fórmula reduzida de Bhaskara:
Lembrando a fórmula:
Substituindo os coeficientes fica:
efetuando as operaçõe indicadas tmos:
Logo o conjunto-verdade da equação é dado por:
V = {1, 3}
Neste exemplo a equação deu origem a dois resultados (2 raízes) possíveis. Nem sempre é assim.
Conforme seja o sinal do discrimenante, teremos três casos para interpretar. Em seguida veremos cada um destes casos.
I. No caso de Δ > 0
Se o discriminante é maior do que zero(positivo), como aconteceu no exemplo que acabamos de estudar, é possível extrair a raiz quadrada de Δ com resultado positivo e não nulo, o que faz com que a equação tenha duas raízes reais.
EXERCÍCIO RESOLVIDO
Resolver a equação 3x2 - 7x + 2 = 0
Solução
Tem-se os coeficientes com os valores: a = 3; b = -7; c = 2
Calculando o valo de Δ temos:
Substituindo na fórmula temos:
Daí V = {1/3,2}
II. N0 caso de Δ = 0
Quando o discriminante é nulo tem-se que Δ = 0 fazendo com que a fórmula para o cálculo da raízes da equação do 2º grau fique reduzida a com resultado único. Concluímos então que quando Δ = 0 a equação do 2º grau terá apenas uma raiz real ( ou raiz dupla) e o conjunto-verdade ficará
V = {-b/2a}
EXERCÍCIO RESOLVIDO
Resolver a equação x2 - 4x +4 = 0
Solução
Temos que:
a = 1; b = -4; c = 4
Vamos calcular o discriminante
Δ = (-4)2 - 4.1.4 => Δ = 16 - 16 => Δ = 0
Substituindo na fórmula teremos:
x = -(-4)/(2.1)
E o conjunto-verdade será:
V = {2}
III. No caso de Δ < 0
Sendo o discriminante negativo, não podemos extrair a raiz quadrada quando o conjunto universo é o conjunto dos reais. Sendo assim, toda equação do 2º grau com discriminante menor do que zero não admite nenhuma raiz real. Conseqüentemente o conjunto-verdade será vazio.
V = { }
ESTUDAR AULA 04
Para voltar ao blog clique em Matemática, um jogo
Para visitar meu canal no YouTube clique em PROF CARLOS SILVA
EQUAÇÕES DO 2º GRAU - GABAITO 02
a) {0,3}
b) {0,7}
c) {0,3}
d) {0,-6}
e) {0,-3}
f) {0,8)
g) {0,4}
h) {0,2}
i) {0,5}
j) {0,2}
Para ver as questões outra vez clique em QUESTÕES PROPOSTAS
Para rever o conteúdo teórico clique em EQUAÇÃO DO 2º GRAU - AULA 02
Para voltar ao blog clique em Matemática, um jogo
Para visitar meu canal no YouTube clique em PROF CARLOS SILVA
b) {0,7}
c) {0,3}
d) {0,-6}
e) {0,-3}
f) {0,8)
g) {0,4}
h) {0,2}
i) {0,5}
j) {0,2}
Para ver as questões outra vez clique em QUESTÕES PROPOSTAS
Para rever o conteúdo teórico clique em EQUAÇÃO DO 2º GRAU - AULA 02
Para voltar ao blog clique em Matemática, um jogo
Para visitar meu canal no YouTube clique em PROF CARLOS SILVA
Resolver as equações da forma ax2 + bx = 0
a) 4x2 - 12x = 0
b) 2x2 - 14x = 0
c) 5x2 - 15x = 0
d) 3x2 + 18x = 0
e) 7x2 + 21x = 0
f) 9x2 - 72x = 0
g) x2 - 4x = 0
h) x(x + 3) = 5x
i) 2x2 = 10x
j) (x + 1)(x - 3) = -3
Para ver o gabarito clique em GABARITO
Para rever o conteúdo teórico clique em EQUAÇÃO DO 2º GRAU - AULA 02
Para voltar ao blog clique em Matemática, um jogo
Para visitar meu canal no YouTube clique em PROF CARLOS SILVA
b) 2x2 - 14x = 0
c) 5x2 - 15x = 0
d) 3x2 + 18x = 0
e) 7x2 + 21x = 0
f) 9x2 - 72x = 0
g) x2 - 4x = 0
h) x(x + 3) = 5x
i) 2x2 = 10x
j) (x + 1)(x - 3) = -3
Para ver o gabarito clique em GABARITO
Para rever o conteúdo teórico clique em EQUAÇÃO DO 2º GRAU - AULA 02
Para voltar ao blog clique em Matemática, um jogo
Para visitar meu canal no YouTube clique em PROF CARLOS SILVA
EQUAÇÕES DO 2º GRAU - GABAITO 01
a){-4, 4}
b)∅
c){-4, 4}
d){-1, 1}
e){-3/2, 3/2}
f){-1/6, 1/6}
g){-4/3, 4/3}
h){-5/4, 5/4}
i) ∅
j) {-3, 3}
Para ver as questões outra vez clique em QUESTÕES PROPOSTAS
Para rever o conteúdo teórico clique em EQUAÇÃO DO 2º GRAU - AULA 02
Para voltar ao blog Matemática, um jogo
Para visitar meu canal no YouTube clique em PROF CARLOS SILVA
b)∅
c){-4, 4}
d){-1, 1}
e){-3/2, 3/2}
f){-1/6, 1/6}
g){-4/3, 4/3}
h){-5/4, 5/4}
i) ∅
j) {-3, 3}
Para ver as questões outra vez clique em QUESTÕES PROPOSTAS
Para rever o conteúdo teórico clique em EQUAÇÃO DO 2º GRAU - AULA 02
Para voltar ao blog Matemática, um jogo
Para visitar meu canal no YouTube clique em PROF CARLOS SILVA
Resolver as equações da forma ax2 + c = 0
a) 4x2 - 64 = 0
b) 5 x2 + 5 = 0
c) -3 x2 + 48 = 0
d) x2 - 1 = 0
e) 4 x2 - 9 = 0
f) 36 x2 - 1 = 0
g) 9 x2 - 16 = 0
h) 25 - 16 x2 = 0
i) 1 + 4 x2 = 0
j) 45 - 5x2 = 0
Para ver o gabarito clique em GABARITO
Para rever o conteúdo teórico clique em EQUAÇÃO DO 2º GRAU - AULA 02
Para voltar ao blog clique em Matemática, um jogo
Para visitar meu canal no YouTube clique em PROF CARLOS SILVA
b) 5 x2 + 5 = 0
c) -3 x2 + 48 = 0
d) x2 - 1 = 0
e) 4 x2 - 9 = 0
f) 36 x2 - 1 = 0
g) 9 x2 - 16 = 0
h) 25 - 16 x2 = 0
i) 1 + 4 x2 = 0
j) 45 - 5x2 = 0
Para ver o gabarito clique em GABARITO
Para rever o conteúdo teórico clique em EQUAÇÃO DO 2º GRAU - AULA 02
Para voltar ao blog clique em Matemática, um jogo
Para visitar meu canal no YouTube clique em PROF CARLOS SILVA
EQUAÇÕES DO 2º GRAU - AULA 02
1. INTRODUÇÃO
EQUAÇÕES COMPLETAS E INCOMPLETAS
1. INTRODUÇÃO
Na aula anterior tratamos da identificação das equações do 2º grau. Neste momento trataremos da classificação das equações do segundo grau como incompletas e completas, reconhecer estes tipos bem como resolver as equações do 2º grau incompleta, em seus 3 casos diferentes. Já a resolução das equações do segundo grau completa será assunto das aulas subsequantes.
2. CLASSIFICAÇÃO DAS EQUAÇÕES DO 2º GRAU
2.1- Uma equação do 2º grau é completa quando, reduzida à forma geral, tem todos os coeficientes diferentes de zero.
2.2- Chama-se incompleta se pelo menos um de seus coeficientes, com exceção de a, é igual a zero.
3. TIPOS DE EQUAÇÕES INCOMPLETAS
As equações incompletas são dos tipos seguintes:
◊ ax2 + bx = 0 quando c = 0
◊ ax2 + c = 0 quando b = 0
◊ ax2 = 0 quando b = c = 0
4. RESOLUÇÃO DAS EQUAÇÕES INCOMPLETAS
Resolver uma equação é achar o seu conjunto-verdade, soluções ou raízes. No campo real o seu conjunto-verdade pode ter um elemento, dois ou mesmo ser vazio.
É importante lembrar que uma raiz (ou solução) de uma equação é um número que, ao ser colocado no lugar de da variável/incógnita, torna a igualdade(sentença) correta.
◊ 4.1- Equação da forma ax2 + c = 0
Lembrando que estas equações acontecem quando o coeficiente b = 0.
Solução
ax2 + c = 0
Transportando a constante “c” para o segundo membro teremos,
ax2 = - c
e dividindo pelo coeficiente “a” resulta:
x2 = - c/a
Se o segundo membro é constituído por um número positivo o conjunto-verdade terá dois elementos os quais serão números reais relativos simétricos.
Veja que, extraindo a raízes quadradas, teremos:
x = ±√(-c/a)
Fazendo, para simplificar, k = - √(-c/a)
teremos: V = { - k , + k }
EXERCÍCIO RESOLVIDO
Exemplo 1:Resolver a equação 5x2- 20 = 0.
Solução
Transportando a constante(o termo independente) para o 2º membro da equação temos:
5x2 = 20
e dividindo pelo coeficiente de x2, temos:
x2 = 20/5
x2 = 4
x = ± √4
donde x = ± 2
Logo V = { - 2, + 2}
Observação: É importante salientar que as soluções de uma equação desse tipo nem sempre são números inteiros.
Veja a equação que segue para exemplificar esta observação:
5x2 - 50 = 0
5x2 = 50
x2 = 50 / 5
x2 = 10
x = ±√10
V = { - √10, √10}
EXERCÍCIOS PROPOSTOS 1
◊ 4.2- Equação da forma ax2 + bx = 0
Solução
Colocando x em evidência, teremos:
x(ax + b) = 0
Aplicando a lei do cancelamento do produto, resulta
x = 0 ou ax + b = 0
A solução x = 0 é um elemento do conjunto-verdade da equação. Da segunda, tiramos:
ax = - b => x = - b/a
Logo, V = {0, -b/a}
EXERCÍCIO RESOLVIDO
Resolver a equação 2x2 - 10x = 0
Fatorando, teremos:
2x(x - 5) = 0 donde
⇒ 2x = 0 ⇒ x = 0
ou
x - 5 = 0 ⇒ x = 5
Concluímos então que V = {0, 5}
EXERCÍCIOS PROPOSTOS 2
◊ 4.3- Equação da forma ax2 = 0
Passando a para o segundo membro da equação temos
x2 = 0/a ⇒
x2 = 0 ⇒
x = ± √0 ⇒
x = ± 0 ⇒
x = 0 Logo,
V = {0}
Para voltar ao blog clique em Matemática, um jogo
EQUAÇÕES DO 2º GRAU - AULA 01
1. INTRODUÇÃO
Não é raro, ao equacionarmos um problema, obtermos uma equação com a incógnita aparecendo elevada ao quadrado. Estas são as chamadas equações do 2º grau.
Eis alguns exemplos:
👉 x2 - 20 = 0
👉4x2 = 100x
👉x2 - 8x + 15 = 0
Observe que em todas as expressões aparece o termo x com o expoente 2.
2. DEFINIÇÃO
Chama-se equação do 2º grau a uma incógnita a toda sentença aberta que é expressa ou pode ser colocada sob a forma
ax2 + bx + c = 0
O número a é o coeficiente de x2.
O número b é o coeficiente de x.
O número c é o termo independente.
onde a é diferente 0 porque, nesse caso, o termo x2 seria eliminado e b, c, são números reais quaiquer.
Na hipótese de acontecer que a = b = c = 0 estaremos diante de um polinômio do segundo grau nulo.
Exemplo 1:
3x2 - 15x + 18 = 0
A expressão acima é uma equação do 2o grau em que identificamos os coeficientes:
a = 3,
b = - 15 e
c = 18
2. OBSERVAÇÕES
A relação (fórmula) ax2 + bx + c = 0
chama-se forma normal ou geral e as letras a, b, c, são os coeficientes ou parâmetros.
Os coeficientes podem ser numéricos ou literais.
Exemplo 2:
Na equação 2x2 + 3x - 8 = 0
temos que identificar os coeficientes:
a = 2,
b = 3 e
c = - 8
Exemplo 3:
Na equação (m-1)x2 + (2m + 3)x + m2 - 6m + 8 = 0
temos que estão como coeficientes:
a= (m - 1),
b= (2m + 3) e
c = (m2 - 6m + 8)
E, neste caso, a = m - 1 deve ser diferente de zero com o que conclui-se que m deve ser diferente de 1.
Recomenda-se que, nas resoluções das equações do 2º grau se trabalhe com o coeficiente de x2 sempre positivo. Caso não o seja, facilitará suas contas, multiplicando-se toda a equação por (- 1) e seus termos mudarão de sinal.
O termo c é chamado de termo conhecido, termo independente ou constante.
Quando os coeficientes são números a equação se diz numérica. Se estes são letras as equações se denominam literais.
Muitas situações aparecerão em que as equações não aparecerão arrumadinhas, bonitinhas. Nestas circunstâncias é necessário reorganizar de modo a se obter uma equação no formato padrão (ax2 + bx + c = 0).
Exemplo 4:
Veja que a equação (2x + 1)² - 5(x - 1) = 0 não está no formato padrão. Para arrumá-la lançamos mão dos conhecimentos de produtos notáveis, ou seja, desenvolvemos o quadrado no primeiro termo e aplicamos a propriedade distributiva no segundo, ficando:
(2x)² + 2(2x)(1) + (1)²- 5(x) - 5(-1) = 0
desenvolvendo as operações indicadas teremos:
4x² + 4x + 1- 5x + 5 = 0 agrupando os termos semelhantes temos:
4x² - x + 6 = 0 que está no formato padrão como queríamos.
Para voltar ao blog clique em Matemática, um jogo
Assinar:
Postagens (Atom)
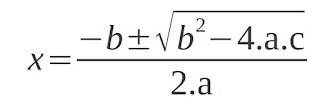

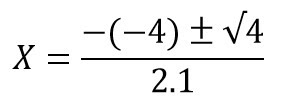
 =>
=> =>
=>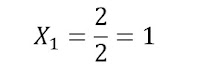 =>
=> =>
=> =>
=>