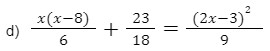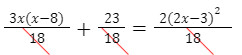Exercícios resolvidos sobre equação do 2º grau 03

EXERCÍCIOS RESOLVIDOS SOBRE EQUAÇÕES DO 2º GRAU INCOMPLETAS

01 - Resolva as seguintes equações do segundo grau com uma incógnita,
sendo U = IR
a. x² - 16x = 0

Solução -

Equação do 2º grau incompleta a qual formalizando fica:
x² - 16x + 0 = 0
a = 1, b = - 16 e c = 0
Nesse caso devemos colocar x em destaque pela operação de evidenciação:
x(x - 16) = 0
o que permite duas possibilidades
I. x = 0 ou
II. x - 16 = 0 ⇒
⇒ x = 16
V = {0, 16}

Respostas:

As possíveis raízes da equação da equação solicitada são 0 e 16.

     

   

 

Solução - 

Primeiro calcula-se o mmc de 6 e 9 que é 18 e usa-se
esse resultado para transformar as frações
da equação para denominadores comuns.

⇒  

⇒ ⇒
⇒ 3.(x + 1)(1 - x) + 4x(x - 4) = 3 ⇒
⇒ 3.(x + 1)[-(x - 1)] + 4x² - 16x = 3 ⇒
⇒ - 3(x + 1)(x - 1) + 4x² - 16x = 3 ⇒
⇒ -3(x² - 1) + 4x² - 16x = 3 ⇒
⇒ - 3x² + 3 + 4x² - 16x = 3 ⇒

 ⇒ 3 + x2 - 16x = 3   ⇒  3   -   3   + x2 - 16x = 0  ⇒

 ⇒ x2 - 16x = 0  Agora vamos por x em evidência

x(x - 16) = 0  ⇒  duas possibilidades

I. x = 0 ou II. x - 16 = 0 ⇒ x = 16

V = {0, 16}

Resposta:

As possíveis raízes da equação da equação solicitada são 0 e 16. 

 

 

c) 4x2 - 48 = 0

Solução - 

 Equação do 2º grau incompleta a qual formalizando fica:

4x2 + 0x - 48 = 0   ⇒

a = 1, b = 0 e c = - 48

4x2 =  48   ⇒

  ⇒ x2 = 48 / 4   ⇒

  ⇒ x2 = 12   ⇒

Resposta
:  

As possíveis raízes da equação da equação solicitada são

  e  .

 

 

 

Solução -

Primeiro calcula-se o mmc de 6, 18 e 9 que é 18

e, em seguida, usa-se esse resultado para transformar as frações da equação
para denominadores comuns.

 

 eliminando os denominadores encontraremos:

eliminando os denominadores encontraremos: 3x(x-8)+ 23 = 2(2x-3)² efetuando as operações indicadas teremos
3x²-24x + 23 = (4x² - 12x + 9)
3x² - 24x + 23 = 8x² -24x + 18 agora vamos transferir todos os termos do 2º membro para o 1º membro da equação
3x² - 8x² - 24x + 24x + 23 - 18 = 0
-5x² -24x + 24x + 5 = 0
-5x² + 5 = 0 equação do 2º grau incompleta em que b = 0.
Isolando o termo em x teremos: -5x² = -5 multiplicando por (- 1) vemos: 5x² = 5 ⇒ x² = 5 / 5 ⇒ x² = 1 ⇒ x = ± √1 ⇒ x= ±1 ⇒

V = {-1, 1}

Resposta:

As possíveis raízes da equação da equação solicitada são - 1 e 1 .

EXERCÍCIOS PROPOSTOS 1


EXERCÍCIOS PROPOSTOS 2



Para voltar ao blog clique em Matemática, um jogo

ESTUDAR AULA 03

Para visitar meu canal no YouTube clique em PROF CARLOS SILVA