1. RESOLUÇÃO DAS EQUAÇÕES COMPLETAS
Para determinar o conjunto-verdade de uma equação do 2º grau recomenda-se transformá-la noutra equivalente de modo a fique positivo e na busca da adequação à fórmula reduzida ao padrão, ou seja, enfatizando que uma equação do segundo grau deve ser escrita como:
ax2 + bx + c = 0
e usa-se então a conhecida fórmula de Bhaskara conforme a figura que segue:
O binômio b2 - 4ac chama-se discriminante e representa-se pela letra grega Δ (lê-se delta). Assim temos:
Δ = b2 - 4ac
A nossa fórmula ficará então:
Este Δ(o discriminante) pode ser positivo, negativo ou nulo. Vejamos como exemplo a equação
(x - 2)2 - 1 = 0
Como se percebe, esta equação não está no formato padronizado sen, portanto, necesário a sua devida organização e, para tanto vamos começar efetuando o quadrado da diferença indicada.
x2 - 2.x.2 + 22 - 1 = 0
x2 - 4x + 4 - 1 = 0
x2 - 4x + 3 = 0
Agora sim, a equção que temos está padronizada e pronta para identificarmos os seus coeficientees que são: a = 1, b = - 4 e c = 3
Podemos, então,substituir os valores do coeficientes na fórmula do cálculo do Δ
Lembrando que : Δ = b2 - 4ac
Δ = (-4)2 - 4.1.3
Δ = 16 - 12
Δ = 4
e, como vemos Δ > 0
Estamos prontos para substituir na fórmula reduzida de Bhaskara:
Lembrando a fórmula:
Substituindo os coeficientes fica:
efetuando as operaçõe indicadas tmos:
Logo o conjunto-verdade da equação é dado por:
V = {1, 3}
Neste exemplo a equação deu origem a dois resultados (2 raízes) possíveis. Nem sempre é assim.
Conforme seja o sinal do discrimenante, teremos três casos para interpretar. Em seguida veremos cada um destes casos.
I. No caso de Δ > 0
Se o discriminante é maior do que zero(positivo), como aconteceu no exemplo que acabamos de estudar, é possível extrair a raiz quadrada de Δ com resultado positivo e não nulo, o que faz com que a equação tenha duas raízes reais.
EXERCÍCIO RESOLVIDO
Resolver a equação 3x2 - 7x + 2 = 0
Solução
Tem-se os coeficientes com os valores: a = 3; b = -7; c = 2
Calculando o valo de Δ temos:
Substituindo na fórmula temos:
Daí V = {1/3,2}
II. N0 caso de Δ = 0
Quando o discriminante é nulo tem-se que Δ = 0 fazendo com que a fórmula para o cálculo da raízes da equação do 2º grau fique reduzida a com resultado único. Concluímos então que quando Δ = 0 a equação do 2º grau terá apenas uma raiz real ( ou raiz dupla) e o conjunto-verdade ficará
V = {-b/2a}
EXERCÍCIO RESOLVIDO
Resolver a equação x2 - 4x +4 = 0
Solução
Temos que:
a = 1; b = -4; c = 4
Vamos calcular o discriminante
Δ = (-4)2 - 4.1.4 => Δ = 16 - 16 => Δ = 0
Substituindo na fórmula teremos:
x = -(-4)/(2.1)
E o conjunto-verdade será:
V = {2}
III. No caso de Δ < 0
Sendo o discriminante negativo, não podemos extrair a raiz quadrada quando o conjunto universo é o conjunto dos reais. Sendo assim, toda equação do 2º grau com discriminante menor do que zero não admite nenhuma raiz real. Conseqüentemente o conjunto-verdade será vazio.
V = { }
ESTUDAR AULA 04
Para voltar ao blog clique em Matemática, um jogo
Para visitar meu canal no YouTube clique em PROF CARLOS SILVA
quarta-feira, 30 de dezembro de 2009
EQUAÇÕES DO 2º GRAU - AULA 03
Assinar:
Postar comentários (Atom)
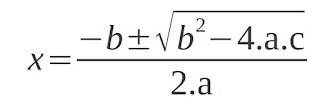

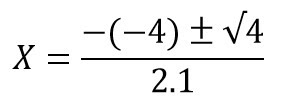
 =>
=> =>
=>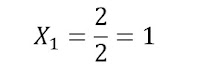 =>
=> =>
=> =>
=>

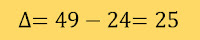


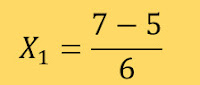

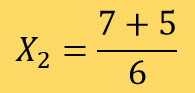
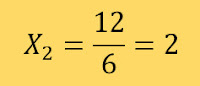
Nenhum comentário:
Postar um comentário