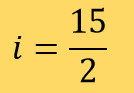1. INTRODUÇÃO
As razões de denominador 100 são chamadas de razões centesimais, taxas percentuais ou simplesmente de porcentagens. As porcentagens costumam ser representadas pelo numerador seguido do símbolo % (onde lê-se "por cento") e significando para cada 100.
👉 As porcentagens também costumam ser expressas sob a forma de decimal, obtida dividindo-se o numerador por 100. Essa é a maneira habitual quando se utiliza uma calculadora.
👉 A porcentagem pode ser utilizada quando queremos expressar alguma quantidade como porcentagem de um valor.
👉 De um modo geral, a% de x, corresponde a multiplicar (a/100) por x.
👉 Lembrando que a porcentagem é calculada multiplicando-se o principal (P), isto é, o elementos de que vamos descobrir a porcentagem, pela taxa (i) e dividindo-se o resultado por 100, ou seja:
i representa a taxa e P representa o principal
👉 Quando ler uma porcentagem pense em para cada 100.
Para voltar ao blog clique em Matemática, um jogo
quinta-feira, 4 de novembro de 2021
Porcentagem 01 - Aula 01
terça-feira, 2 de novembro de 2021
Exercícios resolvidos sobre porcentagem 01
1. INTRODUÇÃO
Lembrando que a porcentagem é calculada multiplicando-se o principal, isto é, o elementos de que vamos descobrir a porcentagem, pela taxa e dividindo-se o resultado por 100, ou seja:
i representa a taxa e P representa o principal(pense em para cada 100)
Eis algumas questões resolvidas:
01) Uma ação de determinada empresa do ramo de aviação que custava R$ 24,00 no início do mês foi adquirida por R$ 22,20 ao final do mesmo mês. Qual a taxa da economia adquirida nessa aquisição?
👉 👉 👉 👉SOLUÇÃO
Observe que nessa aquisição o principal é R$ 24,00 enquanto que a porcentagem/desconto é a diferença entre os valores no início do mês e e o de aquisição no final do mês, ou seja, 24,00 - 22,20 = 1,80
Resposta: A taxa de economia na aquisição foi de 7,5%.
Para voltar ao blog clique em Matemática, um jogo
sábado, 30 de outubro de 2021
Exercícios propostos sobre equações do 2º grau completas 04
Exercícios propostos sobre equações do 2º grau completas 05 Resolver as equações do 2º grau completas que seguem no universo dos reais.
01) 2x2 + 2x = –1
02) 2x2 – (3/2) + (1/4) = 0
03) (2x + 1)2 – 5(2x + 1) + 4 = 0
04) x(x - 2) = 8(x - 1)
05) x2 + (2/3)x + (1/9) = (4/25)
06) x2 + 0,6x = – 0,08
07) (x - 4)2 - (x - 1)2 = 10 - x2
08) (x - 1)/2 - (3x - x2)/3 = x + 1/3
09) x2/3 = 8/3 + x/9
10) (x - 1)2 + (x + 2)2 - 9 = 0
Para ver o resultado destas questões clique em GABARITO 04
Para rever o conteúdo teórico clique em EQUAÇÃO DO 2º GRAU - AULA 02
Para resolver mais questões clique em Exercícios propostos sobre equações do 2º grau completas 02
Para voltar ao blog clique em Matemática, um jogo
Para visitar meu canal no YouTube clique em PROF CARLOS SILVA
sexta-feira, 29 de outubro de 2021
Gabarito dos exercícios propostos sobre equações do 2º grau completas 03
Gabarito dos exercícios propostos sobre equações do 2º grau completas 03
01) Δ = 25; V = { - 2, 3}
02) Δ = 16; V = { - 1, - 1/5}
03) Δ = - 8; V = { }
04) Δ = 400; V = { - 16, 4}
05) Δ = 4; V = { 2, 4}
06) Δ = 36; V = { - 1,5}
07) Δ = 25; V = { 3,8}
08) Δ = 36; V = { 3,9}
09) Δ = 16; V = { 1,5}
10) Δ = 0; V = { 3/2}
Para ver o resultado destas questões clique em GABARITO 01
Para rever o conteúdo teórico clique em EQUAÇÃO DO 2º GRAU - AULA 02
Para resolver mais questões clique em Exercícios propostos sobre equações do 2º grau completas 02
Para voltar ao blog clique em Matemática, um jogo
Para visitar meu canal no YouTube clique em PROF CARLOS SILVA
quinta-feira, 28 de outubro de 2021
Gabarito dos exercícios propostos sobre equações do 2º grau completas 02
Gabarito dos exercícios propostos sobre equações do 2º grau completas 02
1) Δ = 25; V = { - 7, - 2}
2) Δ = 4; V = {3, 5}
3) Δ = 9; V = {4, 7}
4) Δ = 144; V = { - 3, 9}
5) Δ = - 4; V = { }
6) Δ = 144; V = { - 8, 4}
7) Δ = - 3; V = { }
8) Δ = 100; V = { - 3, 7}
9) Δ = 100; V = { 1, 11}
10) Δ = 144; V = {- 11, 3}
Para ver o resultado destas questões clique em GABARITO 02
Para rever o conteúdo teórico clique em EQUAÇÃO DO 2º GRAU - AULA 02
Para resolver mais questões clique em Exercícios propostos sobre equações do 2º grau completas 02
Para voltar ao blog clique em Matemática, um jogo
Para visitar meu canal no YouTube clique em PROF CARLOS SILVA
Exercícios propostos sobre equações do 2º grau completas 03
Resolver as equações do 2º grau completas que seguem no universo dos reais.
01) x2 - x - 6= 0
02) 5x2 + 6x + 1 = 0
03) x2 + 3 - 2x = 0
04) 12x = 64 - x2
05) (x +3) (x - 3) = 6x - 17
06) x(x - 2) + 1 = 2(x + 3)
07) (x - 5)2 = x + 1
08) (x + 3) (x - 3) = 12x - 36
09) (x - 4)2 - (x - 1)2 = 10 - x2
10) 4x2 + 9 = 12x
Para ver o resultado destas questões clique em GABARITO 03
Para rever o conteúdo teórico clique em EQUAÇÃO DO 2º GRAU - AULA 02
Para resolver mais questões clique em Exercícios propostos sobre equações do 2º grau completas 02
Para voltar ao blog clique em Matemática, um jogo
Para visitar meu canal no YouTube clique em PROF CARLOS SILVA
Exercícios propostos sobre equações do 2º grau completas 02
Resolver as equações do 2º grau completas que seguem no universo dos reais.
1) x2 + 9x + 14 = 0
2) x2 - 8x + 15 = 0
3) - x2 + 11x - 28 = 0
4) x2 - 6x - 27 = 0
5) x2 - 6x + 10 = 0
6) x2 + 4x - 32 = 0
7) x2 + x + 1 = 0
8) x2 = 4x + 21
9) x2 = 12x - 11
10) x2 - 33 = - 8x
Para ver o resultado destas questões clique em GABARITO 02
Para rever o conteúdo teórico clique em EQUAÇÃO DO 2º GRAU - AULA 02
Para resolver mais questões clique em Exercícios propostos sobre equações do 2º grau completas 02
Para voltar ao blog clique em Matemática, um jogo
Para visitar meu canal no YouTube clique em PROF CARLOS SILVA
segunda-feira, 25 de outubro de 2021
Exercícios resolvidos sobre equação do 2º grau 02
EQUAÇÕES COMPLETAS E INCOMPLETAS
1. INTRODUÇÃO
No tópico anterior tratamos da identificação das equações do 2º grau. Neste momento trataremos da classificação das equações do segundo grau como incompletas e completas, reconhecer estes tipos bem como resolver as equações do 2º grau incompleta, em seus 3 casos diferentes. Já a resolução das equações do segundo grau completa será assunto dos tópicos subsequentes.
👉 Uma equação do 2º grau é completa quando, reduzida à forma geral, tem todos os coeficientes diferentes de zero.
👉 Chama-se incompleta se pelo menos um de seus coeficientes, com exceção de a, é igual a zero.
👉Resolver uma equação é achar o seu conjunto-verdade, soluções ou raízes. No campo real o seu conjunto-verdade pode ter um elemento, dois ou até mesmo ser vazio.
👉Uma raiz (ou solução) de uma equação é um número que, ao ser colocado no lugar da variável/incógnita, torna a igualdade(sentença) verdadeira.
👉É importante salientar que as soluções de uma equação do 2º grau, completas ou incompletas, nem sempre são números inteiros.
👉As equações incompletas são dos tipos seguintes:
◊ ax2 + bx = 0 quando c = 0
◊ ax2 + c = 0 quando b = 0
◊ ax2 = 0 quando b = c = 0
2. EXERCÍCIOS RESOLVIDOS SOBRE EQUAÇÕES DO 2º GRAU INCOMPLETAS
01 - Resolver a equação 6x2 - 30x = 0 no universo dos reais.
SOLUÇÃO
6x2 - 30x = 0
Percebemos que esta equação é da forma ax2 + bx = 0 tendo, portanto, o coeficiente c = 0.
Observemos ainda que, tanto o termo 6x2 como o termo - 30x são divisíveis por 6x que pode ser colocado em evidência, transformando a expresão da questão em:
6x(x - 5) = 0
6x = 0 => x = 0/6 => x = 0 ou
x - 5 = 0 => x = 5
👉 Resposta: V = {0, 5}
02 - Resolver a equação do 2º grau 3x2 - 12 = 0 no universo dos reais.
SOLUÇÃO
3x2 - 12 = 0
Percebemos que desta vez a equação é da forma ax2 + c = 0 tendo, portanto, o coeficiente b = 0.
Transportando a constante “- 12” para o segundo membro teremos,
3x2 = 12
e agora dividindo pelo coeficiente “3” resulta:
x2 = 12/3
x2 = 4
Como o segundo membro é constituído por um número positivo o conjunto-verdade terá dois elementos os quais serão números reais relativos simétricos.
Veja que, extraindo a raízes quadradas, teremos:
x = ±√ 4
Fazendo, para simplificar, x = ±2
👉Resposta: V = { - 2 , + 2 }
03 - Resolver a equação 5x2 - 125 = 0 tendo como universo o conjunto dos reais.
SOLUÇÃO
5x2 - 125 = 0
Transportando a constante(o termo independente) - 125 para o 2º membro da equação temos:
5x2 = 125
e dividindo pelo coeficiente de x2, temos:
x2 = 125/5
x2 = 25
x = ± √25
donde x = ± 5
👉Resposta: V = { - 5, + 5}
04 - Resolver a equação 10x2 - 200 = 0 usando como universo o conjunto dos reais.
SOLUÇÃO
10x2 - 200 = 0
10x2 = 200
x2 = 200 / 10
x2 = 20
x = ±√20
x = ±√(4 . 5)
x = ±√4 . √5
x = ±2√5
👉Resposta: V = { - 2√5, 2√5}
05 - Resolva a equação 8x2 = 0
SOLUÇÃO
Passando o 8 para o segundo membro da equação temos
x2 = 0/8 ⇒
x2 = 0 ⇒
x = ± √0 ⇒
x = ± 0 ⇒
x = 0 Logo,
👉Resposta: V = {0}
EXERCÍCIOS PROPOSTOS 1
EXERCÍCIOS PROPOSTOS 2
Para voltar ao blog clique em Matemática, um jogo
Para visitar meu canal no YouTube clique em PROF CARLOS SILVA
sábado, 23 de outubro de 2021
Exercícios resolvidos sobre equação do 2º grau 01
1. INTRODUÇÃO
Equações com a incógnita aparecendo elevada ao quadrado. Estas são as chamadas equações do 2º grau.
Eis algumas questões resolvidas:
01) Qual das expressões que seguem não é uma equação do 2º grau?
👉A) x2 - 15 = 0
👉B) 3x2 = 30x
👉C) 3x2 - 24x + 45 = 0
👉D) x-2 - 8x + 15 = 0
SOLUÇÃO
Observe que nas expressões A, B e C aparece o termo x com o expoente 2. No entanto, no item D o expoente de x é - 2 (2 negativo) o que torna esta expressão não ser uma equação do 2º grau.
👉 Resposta certa item D.
02) Apresente a soma dos coeficientes da equação:
5x2 - 12x + 17 = 0
A) 5
B) 10
C) 15
D) 20
SOLUÇÃO
É importante começar identificando a expressão acima como uma equação do 2o grau padronizada em que identificamos os coeficientes:
a = 5,
b = - 12 e
c = 17
Logo a soma será:5 + (- 12) + 17 = 22 - 12 = 10
👉 Resposta certa item B.
03) Na equação 8x2 + x - 7 = 0
Sobre a soma de seus coeficientes podemos afirmar:
A) 1
B) Um número ímpar
C) Um número primo
D) Divisor de 5
SOLUÇÃO
Começamos identificando os seus coeficientes:
a = 8,
b = 1 e
c = - 7
Logo a soma será:8 + 1 + (- 7) = 9 - 7 = 2 que é um número primo
👉 Resposta certa item C.
04) Na expressão (2m-8)x2 + (2m + 1/2)x + m2 - 3m + 15 = 0
calcule o valor de m para que ela represente uma equação do 2º grau.
SOLUÇÃO
Na referida expressão estão como coeficientes:
a = (2m - 8),
b = (2m + 1/2) e
c = (m2 - 3m + 15)
E, neste caso, a condição para que a expressão represente uma equação do 2º grau é que o coeficiente de x2 não seja nulo, ou seja, a = 2m - 8 que deve ser diferente de zero com o que conclui-se que 2m - 8 ≠ 0 => 2m # 8 =. m ≠ 8/2 => m ≠ 4.
👉 Resposta: m deve ser diferente de 4.
05) A soma dos coeficientes da equação do 2º grau (3x - 1)² - 2(x + 5) = 0 será:
A) 4
B) - 4
C) 8
D) - 8
SOLUÇÃO
Veja que a equação (3x - 1)² - 2(x + 5) = 0 não está no formato padrão. Para arrumá-la lançamos mão dos conhecimentos de produtos notáveis, ou seja, desenvolvemos o quadrado da diferença no primeiro termo e aplicamos a propriedade distributiva no segundo, ficando:
(3x)² - 2(3x)(1) + (1)²- 2.(x) - 2(5) = 0
desenvolvendo as operações indicadas teremos:
9x² - 6x + 1- 2x - 10 = 0 agrupando os termos semelhantes temos:
9x² - 8x - 9 = 0 que está no formato padrão como precisávamos.
Logo a soma será:9 + (- 8) + (- 9) = 9 - 17 = - 8
👉 Resposta certa item D.
Para voltar ao blog clique em Matemática, um jogo
Exercícios propostos sobre equações do 2º grau completas 03
Resolver as equações do 2º grau completas que seguem.
10) 4x2 - 4x + 1 = 0
11) x2 + 9x + 14 = 0
12) x2 - 8x + 15 = 0
13) -x2 + 11x - 28 = 0
14) x2 - 6x - 27 = 0
15) x2 - 6x +10 = 0
16) x2 + 4x - 32 = 0
17) x2+ x + 1 = 0
18) x2 = 4x + 21
19) x2 = 12x - 11
20) x2 - 33 = - 8x
21) x2 + 3 - 2x = 0
22) 12x = 64 - x2
23) (x +3) (x - 3) = 6x - 17
24) x(x - 2) + 1 = 2(x + 3)
25) (x - 5)2 = x + 1
26) (x + 3) (x - 3) = 12x - 36
27) (x - 4)2 - (x - 1)2 = 10 - x2
55) determine m na equação: (m – 2)x2 – 3mx + (m + 2) = 0 de modo que ela tenha uma raiz positiva e outra negativa.
56) As raízes da equação x2 – 4x + k = 0 são x1 e x2. Se , qual o valor de k?
a) 9
b) 4
c) 3
d) 2
e) 1
57)
GABARITO
3. a) {2a, -2a} b) {3k,-3k} c) {ab3,-ab3}
d) {2b,-2b} e) {6t2,-6t2} f) {m,-m}
g) {3k,-3k} h) {a,-a} i) {3k,-3k}
j) {2m,-2m} k) {0,a} l) {0,b/2}
m) {0,p/q} n) {0,-4t/3} o) {-k2,k2}
p) {0,2a} q) {0,2a/k } r) {0,p/2}
4. Grupo de equações do 2º grau completas e incompletas 10) {1/2} 11) {-7,-2}
12) {3,5} 13) {4,7} 14) {-3,9} 15) { }
16) {-8,4} 17) { } 18) {-3,7} 19) {1,11}
20) {-11,3} 21) { } 22) {-16,4} 23) {12,4}
24) {-1,5} 25) {3,8} 26) {3,9} 27) {1,5}
28) { } 29) {1/2,1/4} 30) {-8/3,3} 31) {3,6}
32) {-1/6.6} 33){ } 34) {-2,4} 35) {1/3,2/3}
36) {-1/3,2} 37) {3,6} 38){2,3} 39) {-6,7}
40) {-1/2,5} 41) {5,14} 42){-12,8} 43) {3,5}
44) {14,-10} 45){-2,44} 46){2,3) 47) {2,5}
48) {-2,2} 49) {0,5} 50) {3,9} 51) {-10,10}
52) {-2/3,4} 53) {-3,18} 54) {1,2;5}
TESTES DE EXAMES PÚBLICOS
01. (CEFET 2001/II FASE-ADAPTADA PARA OBJETIVA - EXAME DE SELEÇÃO ENSINO MÉDIO) Determine o valor de p para que as raízes a e b da equação 2x2 – px – 1 = 0 satisfaçam a relação a2 + b2 = 1.
a) 0
b) 1
c) 2
d) 3
e) 4
02. (CEFET 2001/Conhecimentos gerais-EXAME DE SELEÇÃO ENSINO MÉDIO - ADAPTADA PARA 5 alternativas) Os valores do parâmetro K, para os quais a equação X2 + X + (K2 − 7K ) = 0 tem uma raiz nula, são:
A) 0 e 7
B) 0 e -7
C) -7 e 7
D) -7 e -7
e) 7 e 7
03. (CEFET 2003/EXAME DE SELEÇÃO ENSINO MÉDIO - CG)Se o inverso multiplicativo de x + 4 é x - 4, com x ≠ ±4, x é um número:
A) natural
B) inteiro negativo
C) racional
D) complexo
E) irracional
04. (CEFET 2003/EXAME DE SELEÇÃO ENSINO MÉDIO - CG)Sejam x1 e x2 as raízes da equação 2x2 -6 x + p - 2 = 0. Se, então P é igual a:
A) 1
B) 3
C) 5
D) 7
E) 8
GABARITO
01. A
02. A
03. E
04. C
Para ver o gabarito clique em GABARITO
Para rever o conteúdo teórico clique em EQUAÇÃO DO 2º GRAU - AULA 02
Para voltar ao blog clique em Matemática, um jogo
Para visitar meu canal no YouTube clique em PROF CARLOS SILVA
Exercícios propostos sobre equações do 2º grau completas 02
Resolver as equações do 2º grau completas que seguem.
01) 4x2 - 4x + 1 = 0
02) x2 + 9x + 14 = 0
03) x2 - 8x + 15 = 0
04) -x2 + 11x - 28 = 0
05) x2 - 6x - 27 = 0
06) x2 - 6x +10 = 0
07) x2 + 4x - 32 = 0
08) x2+ x + 1 = 0
09) x2 = 4x + 21
10) x2 = 12x - 11
4. Gabarito do grupo de equações do 2º grau completas e incompletas:
01) {1/2}
02) {-7,-2}
03) {3,5}
04) {4,7}
05) {-3,9}
06) { }
07) {-8,4}
08) { }
09) {-3,7}
10) {1,11}
Para ver o gabarito clique em GABARITO
Para rever o conteúdo teórico clique em EQUAÇÃO DO 2º GRAU - AULA 02
Para voltar ao blog clique em Matemática, um jogo
Para visitar meu canal no YouTube clique em PROF CARLOS SILVA
sexta-feira, 22 de outubro de 2021
Gabarito dos exercícios propostos sobre equações do 2º grau completas 01
01) Δ = 1; V = {2/3, 1}
02) Δ = 49; V = {- 3, 1/2}
03) Δ = 64; V = {1/3, 3}
04) Δ = 1; V = {1/3, 1/2}
05) Δ = 36; V = {- 1/2, 1/4}
06) Δ = 81; V = {- 1, 7/2}
07) Δ = 121; V = {- 3/2, 1/3}
08) Δ = 1; V = { 2, 3}
09) Δ = 9; V = { 1, 4}
10) Δ = 16; V = {- 1, - 1/5}
Para ver o resultado destas questões clique em GABARITO 01
Para rever o conteúdo teórico clique em EQUAÇÃO DO 2º GRAU - AULA 02
Para resolver mais questões clique em Exercícios propostos sobre equações do 2º grau completas 02
Para voltar ao blog clique em Matemática, um jogo
Para visitar meu canal no YouTube clique em PROF CARLOS SILVA
sábado, 16 de outubro de 2021
Exercícios propostos sobre equações do 2º grau completas 01
Resolver as equações do 2º grau completas que seguem.
* No gabarito apresentamos o valor do delta de cada questão para que no caso de você errar os resultados das raízes não tenha necessidade de revisar os cálculos da questão toda.
01) 3x2 - 5x + 2 = 0
02) 2x2 + 5x - 3 = 0
03) 3x2 - 10x + 3 = 0
04) 6x2 - 5x + 1 = 0
05) 8x2 + 2x - 1 = 0
06) 2x2 - 5x - 7 = 0
07) 6x2 + 7x - 3 = 0
08) x2 - 5x + 6 = 0
09) x2 - 5x + 4 = 0
10) 5x2 + 6x + 1 = 0
Para ver o resultado destas questões clique em GABARITO 01
Para rever o conteúdo teórico clique em EQUAÇÃO DO 2º GRAU - AULA 02
Para resolver mais questões clique em Exercícios propostos sobre equações do 2º grau completas 02
Para voltar ao blog clique em Matemática, um jogo
Para visitar meu canal no YouTube clique em PROF CARLOS SILVA
segunda-feira, 11 de outubro de 2021
EQUAÇÕES DO 2º GRAU - AULA 04
Em nosso cotidiano, a equação do segundo grau tem aplicação crucial. Atrravés da equação do segundo grau encontramos as raízes, discriminante, e outros elementos da função quadrática ou do segundo grau. A função quadrática tem por gráfico uma parábola, ou trecho de parábola, que é a curva descrita, por exemplo, no lançamento e no movimento de projéteis como balas de canhão e foguetes, para presumir o ângulo de reflexão de faróis de carros, conjecturar o ângulo da antena parabólica, entre outras coisas. Nesta aula vamos começar relembrando algumas coisas já referidas nas três aulas anteriores.
De uma maneira geral, denominamos equação do segundo grau com uma única variável a toda expresão matemática que possa ser expressa na forma:
ax2 + bx + c = 0
Em que x representa a variável única e a, b e c representam números reais, com a ≠ 0.
Vamos nos lembrar também da fórmula comumente usada para encontrar as raízes da equação de 2º grau atribuída a Bhaskara:
Lembrando ainda que a ≠ 0 e que o binômio b2 - 4ac chama-se discriminante e é representado pela letra grega Δ (que lemos delta).
Assim temos:
Este Δ pode ser positivo (Δ > 0), negativo (Δ < 0 ) ou nulo (Δ = 0). O que nos leva a pensar que conforme seja o seu sinal, teremos três casos para interpretar.
Se o discriminante é maior do que zero(positivo), é possível extrair a raiz quadrada de Δ o que faz com que a equação tenha duas raízes reais distintas.
Calculando preliminarmente o discriminante podemos antever, antes da resolução da equação, se a dita equação tem raízes reais ou não e, no caso de possuir raízes, se são distintas ou não.
I- Δ > 0 ⇒ ax2 + bx + c = 0 possui duas raízes reais distintas ⇒ o conjunto-verdade da equação será dado por: V = { x1, x2}.
II- Δ = 0 ⇒ ax2 + bx + c = 0 possui apenas uma raiz real ⇒ o conjunto-verdade da equação será dado por: V = { x1}.
III- Δ < 0 ⇒ ax2 + bx + c = 0 não possui raízes reais ⇒ o conjunto-verdade da equação será dado por: V = { }.
Agora vamos avançar nos estudos de equação do 2º grau aprendendo mais alguns truques/atalhos que podem fazer você ganhar tempo em muitas oportunidades.
SOMA E PRODUTO DAS RAÍZES DE UMA EQUAÇÃO
Se a equação do 2º grau estiver na forma padronizada fica viável calcular a soma e o produto das raízes sem a necessidade do cálculo das raìzes. Este processo é conhecido como relações de Girard(1590-1633)
Chamaremos de S a soma das raízes e de P o seu produto o que nos levará a escrever:
S = x1 + x2 ⇒
P = x1 . x2 ⇒
EXERCÍCIO RESOLVIDO 1
Seja a equação a equação x2 - 5x + 6 = 0. Calcule o valor da expressão E
E = (x1 + x2) . (x1 . x2).
Solução
Tem-se que: a = 1; b = - 5; c = 6
Na expressão pedida o primeiro o que está dentro do primeiro par de perenteses corresponde à soma das raízes e no segundo par de parenteses o produto:
E = (x1 + x2) . (x1 . x2)
E = S . P
Temos que nos lembrar que:
Observemos que a = 1 logo:
S = - b ⇒ S = - (-5) ⇒ S = 5 e
P = c ⇒ P = 6
Assim temos que E = S . P ⇒
⇒ E = 5 . 6 ⇒
⇒ E = 30
Resposta: E = 30
EXERCÍCIO RESOLVIDO 2
Escreva a equação x2 + 7x + 12 = 0 na forma fatorada.
Solução
Tem-se que: a = 1; b = 7; c = 12
Como a = 1, a expressão pedida, a forma fatorada da equação do 2º grau, será do tipo:
x2 + bx + c = 0 ⇒ (x - x1) . (x - x2) = 0
Pela expressão da forma fatorada fica revelado que vamos necessitar calcular as raízes da equação originária e, segundo as condições apresentadas; a = 1, equação do 2º grau na forma padrão, números inteiros e pequenos, fica mais prático encontrarmos as raízes pelo processo da soma e produto
Temos que nos lembrar que:
Destacando que a = 1 logo:
S = - b ⇒ S = - (7) ⇒ S = - 7 e
P = c ⇒ P = 12
Assim percebemos que x1 e x2 são dois números que somados dá - 7 e que multiplicados resulta 12 ⇒
⇒ x1 = - 4 e x2 = - 3
Substituindo na expressão da forma fatorada:
(x - x1) . (x - x2) = 0
⇒ [x - (- 4)] . [x - (- 3)] = 0⇒
⇒ [x + 4] . [x + 3] = 0⇒
Resposta: A equação na forma fatorada pedida é (x + 4) . (x + 3) = 0
QUESTÃO RESOLVIDA - BÔNUS -
POTENCIAÇÃO NO CAMPO DOS NATURAIS
(UFMT) Sobre o número natural n = 240 - 1, considere as seguintes afirmativas:
I) n é um múltiplo de 31.
II) n é um múltiplo de 5.
III) n é um número primo.
IV) n é um número par.
Estão corretas as afirmações:
a) III e IV
b) II e III
c) II e IV
d) I e III
e) I e II
Solução
Se numa prova uma questão lhe parecer fora de seus domínios não se espante e comece pelos conhecimentos que você consegue lembrar. Faça de conta que é umprato de canja de galinha quente e inicie matando essa sua fome ingerindo pela parte que deve está mais fria, que deve ser próximo à borda por ter menos quantidade de sopa, tende a esfriar primeiro.
Nesta canja, ops! nesta questão vamos começar anaisando as afirmativas para ver se encontramos alguma absurda de cara.
A afirmativa IV "n é um número par." me parece fácil de julgar.
Se num produto de números naturais um dos fatores for o número 2 o resultado será par.(Uma boa lembrança)
Na expressão n = 240 - 1, percebemos que 240 é uma potência do número 2 ou seja, um produto que só tem o número 2 como fator e repetidas vezes nos permitindo concluir que, com certeza, 240 é par.
Puxando um pouco mais da nossa sabedoria nos deparamos com o fato de que "todo número par diminuído de uma unidade tem como resultado um número ímpar". Isto nos remete à conclusão de que n é ímpar tornando falsa a afirmativa IV e, por consequencia elimminando as alternativas a e c restando apenas apenas as opções b, d e e.
Olhando para a parte potencial da expressão de n e desenvolvendo temos:
240 = 210 . 210 . 210 . 210
Calculando temos que 210 = 1024 ⇒
240 = 1024 . 1024 . 1024 . 1024
Focando só nos algarismos das unidades, 4, temos que:
4 . 4 . 4 . 4 = 256 que termina em 6 logo,
n termina em 6 - 1 = 5
Esticando nossa sabedoria lembramos que todo número terminado em 0 ou 5 é múltiplo de 5.
Agora estamos prontos para afirmar que n = 240 - 1 é múltiplo de 5 tornando a afirmativa II correta ao mesmo tempo que torna a afirmativa III falsa vez que múltuplos de 5, fora o próprio 5, não são primos. Com estas conclusões eliminamos as alternativas b e d sobrando apenas a alternativa e que é a opção correta.
Resposta: alternativa e
-BÔNUS DO BÔNUS -
Com uso da calculadora encontramo que n = 1.099.511.627.775
O qual ao fatorar encontramos:
n = 3.5².11.17.31.41.61 681
Assinar:
Comentários (Atom)